Previous: 6. Data Structures
Next: 8. Pointers
7 Subprograms
When solving a problem, it may be difficult to deal with the solution of the problem because it is too complicated. One usual way to deal a difficult and complicated a problem is to divide it to several smaller problems. Then solve each of the smaller problems separately. It is similar when design a computer program for solving a problem. When a program is too large to write in a single function, it is divided into many subprograms and then write the subprogram separately. In this chapter, we will explain subprograms in C programming language.
In most of the previous examples, we write a program by placing all operations in the main function, int main (void). In fact, most programs will contain a number of subprograms. For example, if a program reads a sequence of 10 elements, sorts these elements, and then prints these elements in the sorted order, its main program can be written as simple as three lines, Lines 4 5o 6, in the following program segment:
|
1 2 3 4 5 6 7 8 9 |
int main (void) { int a[10]; ¡@ read_sequence(a, 10); sort_sequence(a, 10); print_sequence(a, 10); ¡@ return 0; } |
The three statements read_sequence(a, 10), sort_sequence(a, 10), and print_sequence(a, 10) are procedure abstractions, or called functions, of the three operations of reading, sorting, and printing of the sequence of 10 elements, respectively. The implementation of the three procedure abstractions are shown in program selection_sort.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
#include <stdio.h> int main (void) { int a[10]; ¡@ read_sequence(a, 10); sort_sequence(a, 10); print_sequence(a, 10); ¡@ return 0; } |
Function sort_sequence calls another function compare_swap whose implementation is also shown in the above program. A sample run of the program is given below. We will defer explanation of the details program selection_sort.c to the following section.
|
Enter the value element 0:
43 |
There are many advantages to write programs with procedure abstraction. A program is easy to read with abstraction and easy to manage. Also, procedure abstraction enhances modularity and reusability of subprograms.
The syntax of a function definition is as below:
|
type identifier (type parameter1, type parameter2, ¼) { function_body; } |
Mathematically, a function maps values of its parameters to another value. The value that a function mapping to is called a returned value in C programming language. In function definition, the returned value is specified by its data type type at the beginning of a function definition. A function has a name which is specified using identifier. The parameters of a function are given as a list of typed parameters: type parameter1, typey parameter2, ¼. The parameters are enclosed by parentheses, "()", and separated by commas, ",". The last part function_body consists of local variable declaration and statements which are the program code of function implementation. With procedure abstraction, we can write functions of testing even number as below:
|
int evenp (int n) { if (n%2==0) return 1; else return 0; } |
The function is named evenp. The first int specifies that function evenp will return an integer value, in fact, a truth value, 0 or 1. Parameter declaration int n says that function evenp has one parameter and its an integer variable of an integer constant. The parameter value is passed from the calling program unit when evenp is called, or invocated. There are two ways to pass function parameters that will be discussed in the next section. The conditional statement in the curly bracket is the function body. Keyword return returns appropriate values, in this case true (1) or false (0). The returned value is passed back to the calling program unit. Function evenp can be implemented as a single line below:
|
int evenp (int n) {return !(n%2);} |
However, the simplified implementation is, in fact, a "complicated" code because it is sometimes vague in semantics of C programming language.
A function is sometimes declared, not defined, without function body. A function declaration is like a function definition, but without the parameter names and the function body:
|
type identifier (type1, type2, ¼); |
For example, function evenp is declared as:
|
int evenp (int); |
A function can be both declared and defined in separate source code files. But, function definition must be given in some source code, once it is declared. Therefore, a C program can be written as several program files and compiled separately. This is said C programming language supports separate compilation. Separation compilation will make program writing clearer and easier to be managed.
We will use the solution of quadratic equation as an example to explain separate compilation. The roots of a quadratic equation ax2+bx+c=0 are given in the following formula:
![]()
If b2-4ac is greater than or equal to zero, the roots have real values; otherwise, the roots have complex values. Hence, in order to solve a quadratic equation, we will add a complex data type and its arithmetic to the C program. Instead of placing all functions in a single program, we write a program for complex arithmetic operations. To carry out this implementation, a header file is needed to define all data types and declare functions that are exported and used in the program of solving a quadratic equation. Header file complex.h contains a data type definition of complex numbers and declaration of arithmetic operations: addition, subtraction, multiplication, and division.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
typedef struct { |
Note that the header file only declares the four arithmetic operations. Each of the function declaration does not have parameter names and function body. Then, function implementation is written in complex.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
#include <stdio.h> |
First, program complex.c has a line #include "complex.h" (Line 2) which includes the type definition and function declaration with function implementation. In each of the function implementation, parameters are specified as usual. Second, program complex.c does not have a main program. Now, we are ready to write a program of quadratic equation solver, quadratic_equation_all.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
#include <stdio.h>
|
Again, program quadratic_equation_all.c has a line #include "complex.h" (Line 3) which will import data type complex and its arithmetic operations to this program. The main program is written in this program also. Variables root1 and root2 are declared of complex type.
7.3 Parameter Passing in C
Parameters appear in a function definition are called formal parameters and parameters appear in a function call are called actual parameters. In a function call, an actual parameter must have the same data type of its corresponding formal parameter. A programming language usually supports several parameter passing methods for binding actual parameters to formal parameters. C programming language has two parameter passing methods: pass-by-value (or call-by-value) and pass-by-address (or call-by-address) for parameter binding.
Consider the following program pass_by_value.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#include <stdio.h>
|
Parameter a in "void foo(int a)" (Line 3) is a formal parameter of function foo and parameter n of "foo(n)" (Line 10) is an actual parameter of foo. If a formal parameter is declared as a non-location variable, its parameter passing method is pass-by-value. For example, since formal parameter a is an integer data type, its parameter passing will use the pass-by-value method. A pass-by-value formal parameter is allocated a memory space to hold a value of its data type. For a pass-by-value parameter, when a function is called, the value of its actual parameter is copied to the location of the corresponding formal parameter. If the value of the formal parameter is modified in the function body, this modification is limited to the scope of the function, i.e., it does not affect the value of the actual parameter. In program pass_by_value.c, variable n in main is initialized to 10 and it is the actual in function call "foo(n)". In function foo, formal parameter a is assigned to the twice of its value, 20. The output in Line 5 and Line 11 shows that the value of variable n is not changed after the function call to foo. This is illustrated in the following program output.
|
a in foo: 20 |
Let us consider another program pass_by_address.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#include <stdio.h>
|
In this example formal parameter a in "void foo(int *a)" (Line 3) is a pointer to an integer and actual parameter &n of "foo(&n)" (Line 10) is a location of variable n. Both of them have the same data type of address parameter. For a pass-by-address parameter, when a function is called, the variable of an actual parameter is bound to the formal parameter because they are pointers point to the same memory location. Hence, when the value of formal parameter is modified, it also changes the value of the actual variable. In Lines 4 and 5, the access of to the value of a parameter in function foo is dereferenced as *a. In Line 10, when foo is called &n is passed to the formal parameter. Both output of Lines 5 and 11, show the values of *a and n are 20:
|
a in foo: 20 |
Stack Implementation
Next, we will turn to the implementation of stacks. Program stack_array.h is the head file of stack implementation using an array. We set the maximum number of stack elements to 100 and define a symbol max to denote the maximum stack length. The stack is defined defined as a data type with two fields: int element[max], an array holding the stack elements, and int ptr, an index denoting the stack pointer pointing to the top element of the stack. Six functions of stack operations are declared including stack initialization, empty stack testing, the access operation of the stack top element, the stack push operation, the stack pop operation, and the operation of printing all stack elements. Note that the stack parameters are all declared as pass-by-address because some these operations will cause the change of the stack elements and/or the stack top pointer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 19 20 |
#define max 100 ¡@ void printStack(stack *); |
Program stack_array.c is the implementation of stack data type. When the actual parameter is a pointer to a structure, the access to structure fields uses "->", e.g., "s->ptr = -1" in function initialStack, instead of the dotted expression. The assignment "s->ptr = -1" in initialStack simply means that stack is initially set to the empty stack and the pointer points to the position below the bottom element s->elem[0].
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
#include <stdio.h>
printf("%4d", s->elem[i]); |
Program stack_array_reverse.c is a sample application program performing stack reverse operation.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 |
#include <stdio.h>
return 0; |
The output of stack_array_reverse.c is shown below:
|
Print stack s (from top to bottom): |
7.4 Functional Parameters in C
In the cases of pass-by-value and pass-by-address, a
parameter is either a variable or address of a variable. However, in some
programming application, it is sufficient to pass variables to functions. For
example, to compute a summation 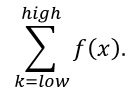 it
is like to call function sigma(low, high, f(x)).
The last parameter is not a variable, but a function which may be a square
function x2, a cubic function
x3, or a polynomial function of x such as f(x)=5x3-2x2+x-6.
That is, f(x) is known as a high-order
parameter, not representing a data variable. C programming language allows this
type of funtional parameter program
functional_parameter.c:
it
is like to call function sigma(low, high, f(x)).
The last parameter is not a variable, but a function which may be a square
function x2, a cubic function
x3, or a polynomial function of x such as f(x)=5x3-2x2+x-6.
That is, f(x) is known as a high-order
parameter, not representing a data variable. C programming language allows this
type of funtional parameter program
functional_parameter.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 25 |
#include <stdio.h> |
In program functional_parameter.c, function sigma() is declared with a function parameter f of type int (*f) (int). This is not a type of data variable, but it is a type of function pointer which is the memory location of a function. Recall that the execution code of a program is also stored in memory. Program functional_parameter.c also declares two functions square() and cubic(). In main(), these two functions are called by sigma() as actual functional parameters, with lower bound 1 and upper bound 10, sigma(1, 10, square) and sigma(1, 10, cubic) and produces the following output:
|
Summation of square 1 to 10: 385 |
A function in C may call other functions, including itself. A function calls it self is called a recursive function. Let use consider a program of computing factorial function, n!, for a positive number n. Mathematically, we know that 1! is 1 and n!=n´(n-1)!, for n>1. Hence, factorial function is a recursive function. The factorial function can be implemented as program factorial_recursive.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 |
#include <stdio.h>
|
Function fact() receives an (positive) integer n and returns n!. The implementation of fact() is exactly like the mathematical function that it returns 1, when n is 1, and returns n*fact(n-1), when n is greater than 1. The execution of fact(a) will call function fact() n times (including fact(a)). For example, if a is 3 in function main(), then fact(3) is called in Line 16. The execution of fact(3) calls fact(2), the execution of fact(2) calls fact(1), and fact(1) returns 1. Hence, function fact() is called three times. When fact(1) returns to the execution of fact(2), its value is multiplied by 2 and the result 2 is returned by fact(2). When fact(2) returns to the execution of fact(3), its value 2 is multiplied by 3 to get value 6. Finally, fact(3) returns 6 to the call in main(). The factorial function can also be implemented as a loop factorial_iterative.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 |
#include <stdio.h>
|
The iterative program of fact(n) actually computes 1´2´3´¼´(n-1)´n. Both recursive and iterative functions of fact() have the following execution example:
|
Enter a
positive integer n:
6 |
Fibonacci Numbers
Another recursive function we will consider is Fibonacci numbers. Mathematically, Fibonacci numbers form a sequence defined by the following recursive function:
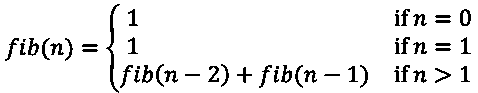
The Fibonacci sequence is obtained as 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ¼. An interesting web site about Fibonacci numbers is referred to http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html. The recursive program of Fibonacci numbers can be implemented as its mathematical definition, fibonacci_recursive.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 |
#include <stdio.h>
while (1) { |
We show a sample run of fibonacci_recursive.c below:
|
input n:
3 |
Fibonacci numbers can be implemented as an iterative loop, fibonacci_iterative.c:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include <stdio.h>
while (1) { |
In the iterative program of fib(n), when n is 0 or 1, it returns 1, respectively, as in the recursive program. When n is greater than 1, we use two variables last1 and last2 to hold the values of fib(k-2) and fib(k-1), respectively, for k iterates from 2 to n. Hence, when k is 2, last1==fib(0)==1 (Line 9) and last2==fib(1)==1 (Line 10), and assign fib(2)==fib(0)+fib(1) to result (Line12). Then last1 and last2 are updated to fib(1) and fib(2) (Lines 13 and 14), respectively, for the next iteration. The loop goes on for fib(3), fib(4), ¼, and up to fib(n). The execution result of fibonacci_iterative.c is identical to that of fibonacci_recursive1.c.
Tower of Hanoi
Tower of Hanoi is an interesting mathematical game invented by Edouard Lucas in 1883. Tower of Hanoi consists of three pegs and a number of discs with different size. Initially, the discs are stacked at a given peg, called the source peg, in the order that the larger discs are under smaller discs. The game is to move one disc from a peg to another one at a time such that after every move the discs on all pegs must be in order. The goal is to move all discs to a peg, called the destination peg. The third peg is called the auxiliary peg. Let the operation of performing Tower of Hanoi be function Hanoi(n, sour, aux, dest), where n is the number discs, and sour, aux, and dest denote the source peg, the auxiliary peg, and the destination peg, respectively. The solution to Tower of Hanoi is given as the following steps:
Perform Hanoi(n-1, sour, dest, aux),
Move disc n from sour to dest, and
Perform Hanoi(n-1, aux, sour, dest).
According to the above solution, we implement program hanoi.c for Tower of Hanoi:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 25 |
#include <stdio.h>
static int step = 1; ¡@
return
0; |
The three pegs sour, aux, and dest are represented using a character. The move of a single disc is describe as an output message. Tower of Hanoi of four discs are shown below:
|
Please enter the number of discs:
4 |
A question is how many steps are needed to move n discs from the source peg to the destination peg. If we assume the number of steps for n disc is f(n), then f(n) is the solution of equation f(n)=2´f(n-1)+1. The solution is f(n)=2n-1. Hence, it takes 7 steps to move 3 discs, 15 steps to move 4 discs, etc.
Previous: 6. Data Structures
Next: 8. Pointers